Resolver un triángulo consiste en calcular
seis elementos: los tres lados y los tres ángulos. Para ello
necesitamos conocer tres de estos seis elementos y uno de los datos por lo
menos sea un lado.
Si el triángulo es rectángulo (un ángulo es 90º) basta conocer dos de sus
elementos, uno de los cuales debe ser un lado.
Se llama razón trigonométrica de un ángulo agudo a cada uno de los
cocientes que se pueden establecer entre los lados de un triángulo
rectángulo cualquiera. Las razones trigonométricas fundamentales (seno,
coseno y tangente) relacionan los ángulos agudos y los lados de un triángulo
rectángulo de la siguiente forma:

Los lados de un triángulo rectángulo verifican el teorema de 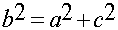 Pitágoras
: Pitágoras
:
Para hallar los ángulos se utilizan las inversas de seno, coseno y tangente
de la siguiente forma:
En la resolución de triángulos rectángulos nos encontramos 4 casos:
1. Se conocen la hipotenusa y un
cateto
y hay que averiguar el otro cateto.

Supongamos que se conoce la hipotenusa  y
el cateto y
el cateto  .
Para encontrar el cateto faltante y los dos ángulos agudos, calculamos .
Para encontrar el cateto faltante y los dos ángulos agudos, calculamos



Otra forma de calcular el cateto  es
mediante el Teorema de Pitágoras es
mediante el Teorema de Pitágoras

Ejemplo: Resolver el triángulo conociendo  y y  . .
Calculamos el cateto faltante y los dos ángulos agudos



2. Se conocen los dos
catetos
y no se conoce la hipotenusa

Para encontrar la hipotenusa y los dos ángulos agudos, calculamos



Otra forma de calcular la hipotenusa  es
mediante el Teorema de Pitágoras es
mediante el Teorema de Pitágoras

Ejemplo: Resolver el triángulo conociendo  y y  . .
Calculamos la hipotenusa y los dos ángulos agudos



3. Se conocen la hipotenusa y un
ángulo agudo

Supongamos que se conoce la hipotenusa  y
el ángulo agudo y
el ángulo agudo  .
Para encontrar el ángulo agudo restante y los catetos, calculamos .
Para encontrar el ángulo agudo restante y los catetos, calculamos



Ejemplo: Resolver el triángulo conociendo  y y  . .
Calculamos el ángulo agudo restante y los catetos



4. Se conocen un
cateto y un
ángulo agudo

Supongamos que se conoce el cateto  y
el ángulo agudo y
el ángulo agudo  .
Para encontrar el ángulo agudo, el cateto restante y la hipotenusa, calculamos .
Para encontrar el ángulo agudo, el cateto restante y la hipotenusa, calculamos



Ejemplo: Resolver el triángulo conociendo  y y  . .
Calculamos el ángulo agudo, el cateto restante y la hipotenusa



|







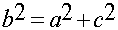
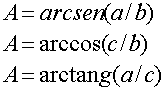
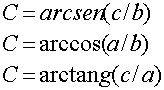

 y
el cateto
y
el cateto  .
Para encontrar el cateto faltante y los dos ángulos agudos, calculamos
.
Para encontrar el cateto faltante y los dos ángulos agudos, calculamos


 es
mediante el Teorema de Pitágoras
es
mediante el Teorema de Pitágoras

 y
y  .
.






 y
y  .
.



 .
Para encontrar el ángulo agudo restante y los catetos, calculamos
.
Para encontrar el ángulo agudo restante y los catetos, calculamos
 y
y  .
.





 y
y  .
.

